El infinito
Ese gran objeto de deseo de los matemáticos y ese gran incomprendido por el resto de la población (aparte del cero) es el infinito. Veamos unas cuantas cosas sobre el infinito:
El concepto del infinito aparece en varias ramas de la matemática, entre otras en la geometría (punto al infinito de la geometría proyectiva), en el análisis matemático (límites infinitos, o límites al infinito) y en los números (ordinales y cardinales) dentro de la teoría de conjuntos. En todos los casos denota
 que el objeto en cuestión no es finito en algún aspecto.
que el objeto en cuestión no es finito en algún aspecto.Los orígenes del símbolo de infinito  son inciertos. Dado que la forma se asemeja a la curva lemniscata (del latín lemniscus, es decir cinta), se ha sugerido que representa un lazo cerrado. Se ha querido ver también una Banda de Möbius en su forma, aunque el símbolo se usó durante cientos de años antes de que August Möbius descubriera la banda que lleva su nombre.
son inciertos. Dado que la forma se asemeja a la curva lemniscata (del latín lemniscus, es decir cinta), se ha sugerido que representa un lazo cerrado. Se ha querido ver también una Banda de Möbius en su forma, aunque el símbolo se usó durante cientos de años antes de que August Möbius descubriera la banda que lleva su nombre.
También se cree posible que la forma provenga de otros símbolos alquímicos o religiosos, como por ejemplo ciertas representaciones de la serpiente Ouroboros.
En la literatura matemática, John Wallis es el primero en usar el símbolo  para representar al infinito en su tratado De sectionibus conicus de 1655.
para representar al infinito en su tratado De sectionibus conicus de 1655.
Los conjuntos finitos tienen una propiedad "intuitiva" que los caracteriza, dada una parte propia de los mismos, ésta contiene un número de elementos menor que todo el conjunto. Es decir, no puede establecerse una biyección entre una parte propia del conjunto finito y todo el conjunto. Sin embargo, esa propiedad "intuitiva" de los conjuntos finitos no la tienen los conjuntos infinitos, formalmente decimos que:
- Un conjunto
 es infinito, si existe un subconjunto propio
es infinito, si existe un subconjunto propio 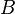 de
de  , es decir, un subconjunto
, es decir, un subconjunto 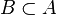 tal que
tal que 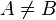 , tal que existe una biyección
, tal que existe una biyección  entre
entre  y
y 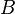 .
.
La noción de cardinalidad de un conjunto, se basa en la noción anterior de biyección. De dos conjuntos entre los que se puede establecer una biyección se dice que tienen la misma cardinalidad. Para un conjunto finito su cardinalidad puede representarse por un número entero. Por ejemplo, el conjunto {Manzana, Pera, Durazno} tiene 3 elementos. Esto significa de modo más formal que se puede establecer una biyección entre tal conjunto y el conjunto {1,2,3}:
Dicho de otra forma, es posible hacer parejas (1, Manzana), (2, Pera), (3, Durazno) de modo que cada elemento de los dos conjuntos sea usado exactamente una vez. Cuando es posible establecer tal relación "uno a uno" entre dos conjuntos se dice que ambos conjuntos tienen la misma cardinalidad, lo cual, para conjuntos finitos, equivale a que tengan el mismo número de elementos.
La primera de finición positiva de conjunto infinito fue dada por Georg Cantor y se basa en la siguiente observación: Si un conjunto S es finito y T es un subconjunto propio, no es posible construir una biyección entre S y T. Por ejemplo, si S = {1,2,3,4,5,6,7,8} y T = {2,4,6,8} no es posible construir una biyección entre S y T, porque de ser así tendrían la misma cardinalidad (el mismo número de elementos).
finición positiva de conjunto infinito fue dada por Georg Cantor y se basa en la siguiente observación: Si un conjunto S es finito y T es un subconjunto propio, no es posible construir una biyección entre S y T. Por ejemplo, si S = {1,2,3,4,5,6,7,8} y T = {2,4,6,8} no es posible construir una biyección entre S y T, porque de ser así tendrían la misma cardinalidad (el mismo número de elementos).
Un conjunto es infinito si es posible encontrar un subconjunto propio del mismo que tenga la misma cardinalidad que el conjunto original. Consideremos el conjunto de los números naturales N={1,2,3,4,5,...}, el cual es un conjunto infinito. Para verificar tal afirmación es necesario encontrar un subconjunto propio y construir una biyección entre ambos. Para este caso, consideremos el conjunto de enteros positivos pares P={2,4,6,8,10,...}. El conjunto P es un subconjunto propio de N, y la regla de asignación  es una biyección:
es una biyección:
ya que a todo elemento de N le corresponde un único elemento de P y viceversa.
De manera relacionada con el infinito para números reales, algunos lenguajes de programación admiten un valor especial que recibe el nombre de infinito: valor que se puede obtener como resultado de ciertas operaciones matemáticas no realizables, tales como las descritas en el punto anterior u operaciones teóricamente posibles, pero demasiado complejas para su trabajo en el ordenador/lenguaje en cuestión. En otros lenguajes simplemente se produciría un error.He recortado un poco el artículo que era de la Wikipedia, si tenéis más interés en el tema (que es bastante interesante y a veces toca un poco con la filosofía) podéis mirar en este enlace donde vienen las propiedades y más links donde mirar más cosas si os da curiosidad.














1 Comments:
Ya decía yo, este hombre sabe algo que yo no. ¿Qué tal algo sobre el teorema de Godel?
Publicar un comentario
<< Home